Прежде чем играть в лотерею, рассчитайте соотношение риска и доходности
Если вы не прочь сыграть в азартные игры, в том числе купить лотерейный билет, разумно сосредоточить свои усилия на том, чтобы получить наибольшую потенциальную доходность при этом имея минимально возможный риск.

В следующих строках попытаемся рассчитать отношение риска к доходности – терминов из инвестиционной деятельности, и традиционно не применяемой в азартных играх.
Есть несколько способов определить лотереи, в которых стоит принять участие.
Основной, наиболее очевидный способ, который придет многим на ум – это выбрать лотерею в соответствии с вероятностями выигрыша в ней.
Однако коэффициенты вероятности выигрыша дают не полный ответ, поскольку они не принимают во внимание размер приза.
Хотя у вас может быть больше шансов выиграть подарочную карту на 500 рублей, чем дом мечты за миллион долларов или джек-пот крупной лотереи, выигрыш подарочной карты будет лишь приятным бонусом, в то время как по-настоящему крупные выигрыши смогут изменить вашу жизнь.
С другой стороны, когда шансы на выигрыш составляют 100 миллионов к одному, вы рискуете стать жертвой лотереи, прежде чем выиграть приз.
Когда мы подразумеваем лотереи, в которых необходимо платить за участие, обращать внимание на вероятности выигрыша, конечно, стоит. Прежде чем тратить своим заработанным трудом деньги узнайте, какие шансы имеются на выигрыш в данной лотерее. Здесь также пригодится знание соотношения риска и доходности.
Что такое соотношение риска и доходности
Соотношение риска и доходности – это простой, но научный способ оценить, окупится ли риск для вас. Эта концепция пришла из инвестиционного мира, но ее можно адаптировать для оценки различных азартных игр, чтобы понять, какие из них вам подходят.
Самый простой способ расчета – это разделить сумму потенциального выигрыша на стоимость игры (в случае лотерей – это будет стоимость одного лотерейного билета).
Чем меньше полученное число – тем меньше риск. Многие инвесторы считают, что риск не имеет смысла, пока соотношение не достигнет значения 2:1. Если значение дроби выше единицы ваш риск выше, чем прибыль, которую вы можете потенциально получить от игры.
Когда дело доходит до азартных игр, это простое соотношение риска и вознаграждения отлично подходит для расчета. Например, вы думаете, стоит ли принимать участие в розыгрыше лотереи в вашем местном клубе по кройке и шитья. Билеты стоят 2 рубля за штуку, а приз – подарочная карта на 100 рублей. Соотношение риска и доходности будет равно 2/100 или 0.02. Это соотношение хорошее и низкое.
У государственных лотерей и других известных мировых лотерей соотношение риска и вознаграждения будет еще более впечатляющим.
Этот метод оценки риска имеет ограниченную полезность для людей, участвующих в розыгрыше лотереи, поскольку он не учитывает вероятность выигрыша.
В то время как соотношение риска и доходности сигнализирует о необходимости участия в лотерее, шансы на выигрыш стремительно стремятся к нулю.
Таким образом, еще один способ применить базовое соотношение риска и вознаграждения к лотерейным покупкам – это считать вознаграждение равным нулю, после чего становится ясно, что математически покупка билетов – пустая трата денег. Но такой образ мышления не поможет, если вы все же решили сыграть в лотерею, но хотите знать, какие именно лотереи имеют наибольший потенциал.
Если вы хотите лучше понять, в какие азартные игры играть, вам необходимо учесть призовую сумму и вероятность выигрыша в расчетах риска и доходности.
Формула, которой вам нужно будет следовать для этого расчета:
Расчетная доходность = (шансы на выигрыш, выраженные в десятичной дроби) x (размер приза)
Модифицированный расчет риска и доходности = (стоимость игры) / (расчетная доходность)
Пример расчета
В качестве примера расчёта возьмем лотерею 5 из 36, шансы на выигрыш в лотерею фиксированы и не зависят от количества купленных билетов. В этом примере, мы предположим, что джек-пот составляет 1000000 (один миллион) рублей.
Шансы на выигрыш этого джек-пота составляют 1:376992, с некоторым округлением это означает, что шанс на победу 0.00000265. Умножим это значение на возможную доходность в размере джек-пота. Умножьте выплату джек-пота в один миллион рублей на этот процент, и вы получите разумное значение для предполагаемой доходности: 2,65.
Когда вы применяете соотношение риска к вознаграждению и делите стоимость билета (40 рублей) на расчетное вознаграждение (2,65 рубля) вы получаете соотношение риска к доходности 15,1.
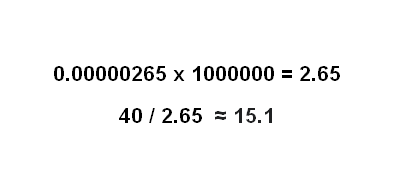
Поскольку это число больше единицы, вы можете видеть, что вы пересекли порог, при котором расчетная выплата превышает ваши инвестиции в билеты.
Конечно, соотношение риска и вознаграждения при игре в 5 из 36 рассчитывается на самом деле сложнее, чем в примере, поскольку лотерея имеет гораздо больше выплат, чем просто джек-пот, и каждая потенциальная выигрышная категория имеет свои собственные вероятности.
Как использовать модифицированное соотношение риска и прибыли
Неудивительно, что расчет риска и доходности за игру в лотерею 5 из 36 не в вашу пользу.
То же верно и для всех азартных игр, в том числе, таких как рулетка или блэк-джек. Отсюда возникла и поговорка: «казино всегда в выигрыше».
Нет причин тратить деньги на лотерейный билет, если вы понимаете, что наиболее вероятным исходом будет потеря денег. С другой стороны, потраченные несколько десятков рублей дают надежду мечте о богатстве, кто-то обязательно выиграет крупную сумму.
Эти расчеты могут помочь вам решить, на что лучше потратить свое время и деньги. Если вы думаете, в какую лотерею сыграть вот вам научный способ сравнения лотерей.
Чем меньше полученное значение расчетной доходности по лотереи тем, лучше потенциальная доходность вложения в игру в лотерею при минимальном риске.
Обратите внимание, чт эти расчеты не увеличивают ваши шансы на победу относительно других участников лотереи и относятся только к финансовому риску. Когда вы участвуете в других типах лотерей, в том числе во всевозможных мотивирующих квестах – вы подвергаетесь другому риску, поскольку ваше время и энергия также имеют ценность.
Хорошая идея создать такую стратегию для игры в лотереи, которая уравновешивает вероятности выигрышей больших призов, но с низкими шансами на выигрыш с выигрышами с большими вероятностями, но меньшими суммами выигрышей, чтобы вы могли выигрывать достаточно часто небольшие суммы, чтобы чувствовать, что ваше время в погоне за джек-потом не потрачено зря.


Немного поспорю с автором. Уверен, что если грамотно учитывать риски, то шансы на выигрыш увеличиваются.
Конечно, риски и доходность всегда просчитывают. Без этого любая лотерея прогорит. И конечно, вопрос всегда – какая структура выигрышей
Есть такая теория вероятности по которой риску учитываются 1:1. То есть 50 на 50. Как не учитывай риски мимо этого научного факта не пройдешь.
Статистику соотношения лучше вообще не проводить, потому что выиграть шансы всегда в разы меньше, нежели шанса проиграть свой капитал. Глубоко мыслить не нужно, просто вспомните сколько раз вы играли в лотерею, посчитайте количество раз, а соотнесите выигрыши и проигрыши.