Самый популярный способ оценки данных при размещении ставок на тотал заключается в использовании среднего значения, но приносит ли это пользу? Статистика имеет два показателя – мода и медиана, которые обычно являются более подходящей альтернативой арифметическому среднему, поэтому крайне важно разобраться в этих понятиях для успешного размещения ставок.
Многие игроки, делающие ставки на тотал в спортивных событиях, используют среднее значение для статистического расчета результатов. Это довольно простой способ. Но многие из них знают о его недостатках?
Например, при размещении ставок на тотал в футболе (общее количество голов) игроки могут придерживаться того мнения, что подсчет среднего количества голов, забитых во время предыдущих игр, позволяет точно определить ожидаемое число голов для следующего матча. Но так ли эффективен подсчет со средними значениями?
Среднее значение дает общее представление о ситуации в ставках на тотал, но при этом не учитывает форму распределения
Среднее значение не самый надежный средний статистический показатель. К примеру, зарплата начальника 95 тысяч рублей, а дворника 5 тысяч, их средняя зарплата на двоих 50 тысяч. Но вернемся к футболу, здесь ситуация примерно такая же.
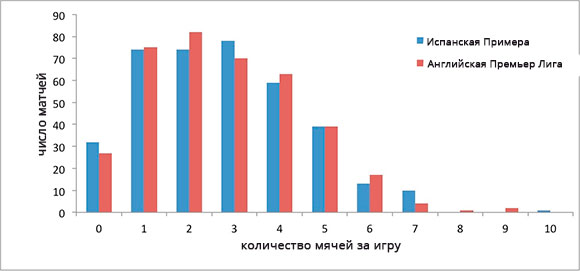
Например, сравним количество голов, забитых в рамках лиг Английской Премьер Лиги (АПЛ) и Испанской Примеры на протяжении сезона 2013/2014 гг. Среднее количество голов из расчета на одну игру для каждой лиги составляет 2,77 и 2,75 соответственно. В итоге игроки могут прийти к выводу о том, что игры в рамках Испанской Примеры чаще заканчиваются с результатом, не превышающим 2,5 гола, по сравнению с АПЛ. Однако это не так – 48,4 % игр английской Премьер Лиги приносят меньше 2,5 гола. Аналогичный показатель для АПЛ составляет 47,3 %.
На нижеприведенной диаграмме видно, что при одинаковом числовом распределении для английской Премьер-лиги чаще всего достигается результат в два гола за игру, а для испанской Примеры – три гола. Среднее значение скрывает этот факт. Этот факт также проявляется и при ставках на тотал в других видах спорта: теннисе, баскетболе, волейболе и др.
Почему происходит именно так? Хотя среднее значение и дает общее представление о ситуации, но при этом не учитывается форма распределения.
Средние величины рискованно использовать, например, при оценке гандикапов для слабых сборных во время международных футбольных турниров, которые считаются аутсайдерами, для каждого квалификационного раунда. Но так ли плохо обстоят дела в действительности? При вычислении среднего количества голов сборных за одну игру можно получить большие итоговые показатели, но они могут существенно измениться с учетом более редких серьезных поражений и привести к тому, что игроки переоценят ожидаемое количество голов.
Ниже приведен анализ альтернатив среднему значению (мода и медиана) с использованием трех наборов чисел для рассмотрения двух вариантов развития событий, при которых среднее значение может стать неприемлемым.
Рассмотрим нижеприведенные наборы чисел (среднее значение каждого
- Набор А: 4, 5, 5, 5, 6.
- Набор Б: 3, 4, 4, 4, 10.
- Набор В: 3, 4, 5, 6, 7.
Первый вариант развития событий. Резко отклоняющиеся значения в начале и в конце
Несмотря на то, что три набора чисел характеризуются одинаковым средним значением и в сумме дают 25, их распределение весьма различное.
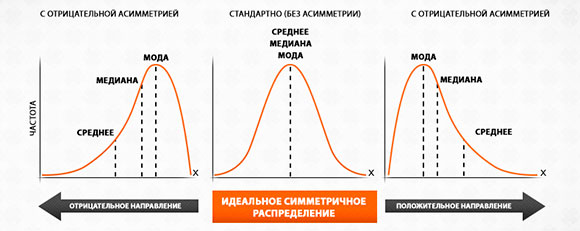
Набор A можно отнести к симметричному распределению (равномерный показатель в начале и в конце, поскольку 4 ниже среднего значения, а 6 – выше).
Среднее значение – это идеальный вариант при наличии симметричного распределения, когда значения переменных возникают с одинаковой частотой в начале и в конце указанного набора. Среднее значение приведено посередине набора.
В свою очередь, набор Б содержит четыре числа ниже среднего значения – только одно число превышает среднее значение. В данном случае возникает несимметричное распределение.
Разобравшись в недостатках метода с использованием среднего значения, можно принимать более взвешенные решения относительно его применения при прогнозировании результатов.
При использовании большого набора данных игроки могут проверить эффективность среднего значения с помощью других показателей – медианы и моды.
Медиана – это значение, занимающее среднее положение в распределении при группировке в возрастающем или убывающем порядке. В последовательностях А и Б это 5 и 4 соответственно.
Мода – это наиболее часто встречающееся значение – 5 и 4 соответственно.
При симметричном распределении среднее арифметическое, медиана и мода должны быть одинаковыми. Различие между двумя последними значениями и средним арифметическим в наборе Б указывает на то, что это несимметричное распределение, и, следовательно, среднее значение – не самый лучший вариант в этом случае.
Второй вариант развития событий. Различный разброс значений
Два набора чисел могут быть симметрично распределены, имея различный разброс значений. Например, набор В симметрично распределен, как и набор А, из-за равномерного уменьшения или повышения чисел в начале и в конце набора с учетом среднего значения.
Поскольку в итоге мы получаем среднее значение, равное 5, это среднее значение больше подходит для набора А, поскольку он содержит больше чисел, более близких к среднему арифметическому. Разница между двумя наборами состоит в разбросе значений в группе. Поэтому необходимо определить разброс значений.
С этой целью игроки могут рассчитать размах и среднеквадратическое отклонение. Размах – разность между максимальным и минимальным значениями – можно легко рассчитать. С другой стороны, вычисление среднеквадратического отклонения – это более сложная задача. В этой статье достаточно указать, что таким образом определяется вариация в наборе данных с учетом среднего значения.
Величина размаха для наборов А и В составляет 2 и 4, а среднеквадратическое отклонение – 0,71 и 1,58 (соответственно). Обе величины больше для набора В – это еще один показатель того, что в последней группе наблюдается более существенное различие.
Вывод
Разобравшись в недостатках метода с использованием среднего значения (несимметричные распределения и различный разброс значений), игроки смогут принимать более взвешенные решения относительно его применения при прогнозировании результатов в ставках на тотал. Тщательный анализ применимости среднего значения не был проведен, однако представленных данных должно быть достаточно для предостережения и напоминания об имеющихся других показателях.
Доминик Кортис, перевод PinnacleSports.
Бонусы букмекерских контор до 16000 рублей от официальных букмекеров

Как правило, для таких сложных рассчетов у большинства игроков просто не хватает времени. Хотя знаю тех, к тов Экселе или других форматах делают небольшие программы-подсказки для себя.
Глупо делать ставки наобум, на “чуйке”. Хотите на тотализаторах именно зарабатывать, а не надеяться на чудо – изучайте всю статистику и вообще любую доступную информацию.
И все же фактор случайности тоже нельзя исключать. Команда может обстучать все стойки, или вратарь соперников поймать кураж и поймать вообще все, что можно – и никакие выкладки не помогут!
Важно изучать не только текущую форму противников, но и историю их противостояний. Бывает так, что в игре принципиальных соперников клубы играют более агрессивно.
Сейчас, когда погода резко испортилась, и на поле сложно даже просто ходить, а не бегать, логично ставить на тотал меньше. Намного сложнее в болоте забивать голы!
Математика – точная наука с ней не поспоришь. Однако на мой взгляд без везения и фарта даже смысла нет пробовать, а иначе Вам удачи не ведать.